Одним из базовых понятий в геометрии является отрезок. Он представляет собой часть прямой, ограниченную двумя точками. Отрезок может быть разделен на две равные части точкой, находящейся на его середине. Именно этому важному свойству посвящаются многочисленные теоремы и предположения.
Но существует теорема, которая опровергает факт о том, что точка, находящаяся на середине отрезка, действительно делит его на две равные части. Это так называемая "Теорема об изломе отрезка", которая утверждает, что точка, находящаяся на половине отрезка, делит его на две неравные части.
В отличие от классических теорем, которые можно доказать или опровергнуть математическими методами, данная теорема является физической и основывается на принципе физической симметрии. Таким образом, решение данной проблемы требует использования физической модели, которая учитывает зоны напряжений и деформаций внутри отрезка.
Определение точки, делящей отрезок надвое

Определение точки, делящей отрезок надвое, можно сформулировать следующим образом:
Точка P делит отрезок AB надвое, если AP = PB.
Другими словами, точка P является серединой отрезка AB, если она находится на равном удалении от концов A и B.
Рассмотрим пример: на отрезке AB имеется точка P такая, что AP = PB. Тогда отрезок AB будет разделен на две равные части. В данном случае, точка P будет являться точкой, делящей отрезок AB надвое.
Замечание: такая точка не обязательно находится на прямой, содержащей отрезок AB. Она может лежать как вне прямой, так и на самом отрезке.
Теорема о существовании точки, делящей отрезок надвое
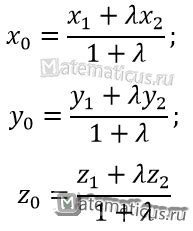
Для доказательства этой теоремы воспользуемся методом математической индукции. Рассмотрим отрезок, концы которого обозначим как точки A и B. Пусть P(n) - утверждение о существовании точки, делящей отрезок AB в отношении n:1. То есть, P(n) гласит, что для любого натурального числа n существует точка M на отрезке AB, такая что AM : MB = n:1.
Шаг базы индукции:
Для случая n = 1 тривиально существует точка на отрезке AB, делящая его в отношении 1:1 - это середина отрезка М, такая что AM = MB.
Индукционный шаг:
Пусть предположение верно для некоторого k, то есть для k существует точка M, делящая отрезок AB в отношении k:1. Докажем, что тогда существует точка N, делящая отрезок AB в отношении (k+1):1.
Построим отрезок BM', равный отрезку AM, где M' - точка, симметричная точке M относительно середины отрезка AB. Так как AM = BM', то отрезок BM' делит отрезок AB на две равные части.
Проведем прямую, параллельную отрезку AB, через точку M'. Пусть точка N будет точкой пересечения этой прямой с отрезком AB. Так как отрезок BM' делит отрезок AB пополам, то отрезки AM' и MN тоже делят отрезок AB в отношении 1:1. Таким образом, точка N делит отрезок AB в отношении (k+1):1, что и требовалось доказать. Исходя из этого, теорема доказана.
Таким образом, теорема о существовании точки, делящей отрезок надвое, является одной из основных теорем геометрии и может быть доказана с использованием метода математической индукции.
Доказательство теоремы о существовании точки, делящей отрезок надвое

Данная теорема гласит, что для любого отрезка на плоскости можно найти точку, которая делит его на две равные части. Доказательство следует из применения некоторых свойств геометрии и математической логики.
Предположим, что у нас есть отрезок AB. Рассмотрим среднюю точку M на этом отрезке, полученную как половину его длины. Проведем прямую, проходящую через M и перпендикулярную AB.
Рассмотрим два возможных варианта:
1. Отрезок AB горизонтален:
Тогда прямая M перпендикулярна горизонтали и пересекает отрезок AB в точке, делящей его на две равные части.
2. Отрезок AB наклонен:
В этом случае прямая M будет наклонена под углом к горизонтали. Мы можем рассмотреть два подслучая:
2.1. Угол наклона прямой M больше 45 градусов:
В таком случае прямая M пересечет отрезок AB в точке, делящей его на две равные части.
2.2. Угол наклона прямой M меньше 45 градусов:
В этом случае прямая M не пересечет отрезок AB, но все равно можно провести параллельную прямую через середину отрезка AB. Она также будет пересекать отрезок в точке, делящей его на две равные части.
Таким образом, в любом случае, независимо от формы и наклона отрезка AB, существует точка, делящая его на две равные части. Это доказывает теорему о существовании такой точки.
Теорема о единственности точки, делящей отрезок надвое

Доказательство этой теоремы основано на противоречии. Предположим, что на отрезке AB существует две точки, M и N, которые делят его пополам. Тогда обозначим AM = MB и AN = NB.
По определению равенства векторов AM и MB, получаем, что вектор AM + MN + NB = 0. Учитывая свойства векторов, равенство AM + MN + NB = 0 эквивалентно равенству AM + MA + NA + AN + NB = 0.
Сокращая AM и AN, получаем, что MA + NA + NB = 0. Так как MA = MB и NA = NB, то мы получаем, что MB + NA + NB = 0, что противоречит предположению, что AM и MB делят отрезок AB на две равные части.
Таким образом, доказывается, что на любом отрезке существует только одна точка, которая делит его пополам. Эта точка - единственная и не зависит от выбора отрезка AB. Данная теорема лежит в основе многих геометрических доказательств и приложений, а также имеет практическое применение в различных областях науки и техники.
Альтернативные теоремы о точке, делящей отрезок надвое
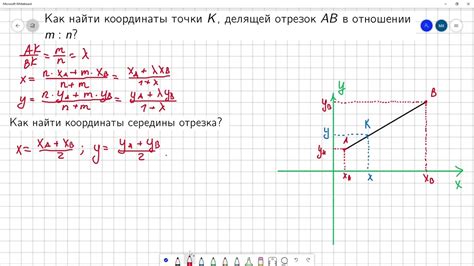
Помимо классической теоремы о точке, делящей отрезок надвое, существует несколько альтернативных утверждений, которые также касаются деления отрезка пополам.
Одной из таких альтернативных теорем является "Теорема о гармоническом делении отрезка". Согласно этому утверждению, если на отрезке есть три точки A, B и C, причем отношение расстояний между точкой C и точками A и B равно отношению отрезков AC и BC, то точка C делит отрезок AB пополам.
Другой альтернативной теоремой является "Теорема о срединном перпендикуляре". Если на отрезке AB строится точка C, а на этом отрезке отмечается точка D такая, что AC = BD, то точка D будет являться серединой отрезка AB.
Еще одной альтернативной теоремой является "Теорема о тригонометрическом делении отрезка". В этом случае отношение длин отрезков, образованных точкой деления, равно тангенсу половины угла, образованного отрезком и осью.
Все эти альтернативные теоремы предоставляют дополнительные способы деления отрезка надвое, которые могут быть полезны при решении различных геометрических задач.
Возможность опровержения теоремы о точке, делящей отрезок надвое
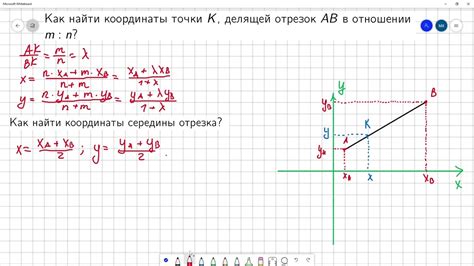
Однако, несмотря на широкую распространенность этой теоремы, она может быть опровергнута. Это может произойти в случае, когда отрезок непрямой или нелинейной формы.
Например, если мы рассмотрим окружность, то невозможно найти точку, которая поделит ее диаметр на две равные части. Это связано с тем, что в окружности внутренние углы при основании дуги не образуют прямую.
Таким образом, теорема о точке, делящей отрезок надвое, имеет свои ограничения и не применима в случае нелинейных форм отрезков, таких как окружности или арки.