Нули функции – одна из основных понятий математического анализа. Понимание этого термина необходимо для решения широкого спектра задач, связанных с изучением поведения функций в различных контекстах. В этой статье мы рассмотрим, что такое нули функции, как их определить и как найти приближенное значение нулей с помощью различных методов.
Нулем функции называется такое значение аргумента, при котором значение самой функции равно нулю. Математически это обозначается как f(x) = 0. Нули функций играют важную роль в практическом применении математического анализа, поскольку позволяют найти точки пересечения графиков функций с осью абсцисс, решить уравнения и системы уравнений, а также анализировать поведение функций в различных интервалах.
Существуют различные методы поиска нулей функций, в зависимости от характеристик исследуемой функции и доступных ресурсов. К некоторым из наиболее распространенных методов относятся метод половинного деления, метод хорд и метод Ньютона. Каждый из этих методов имеет свои особенности и область применения. В этой статье мы рассмотрим основные идеи и принципы работы каждого из этих методов и покажем, как их применять на конкретных примерах.
Определение нулей функции

Нулями функции называются значения аргументов, при которых функция принимает значение 0. То есть, если дана функция f(x), то нули функции могут быть найдены, решив уравнение f(x) = 0.
Нули функции часто называют также корнями или точками пересечения графика функции с осью абсцисс. Они являются важным понятием в математике и находят применение в различных областях, включая физику, экономику, программирование и т. д.
Существует несколько подходов к нахождению нулей функции, в зависимости от её типа и доступности аналитического решения. Классические методы включают методы бисекции, интерполяции, итерации и др.
Определение нулей функции имеет важное значение при решении уравнений и систем уравнений, а также в оптимизации функций и анализе графиков и поверхностей.
Почему нули функции важны
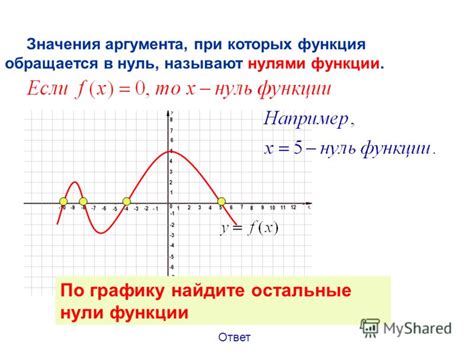
Одна из главных причин, почему нули функции важны, - это то, что они помогают нам найти решения уравнений. Если у нас есть уравнение, то нули функции представляют собой его решения. Поэтому, чтобы найти значения переменных, при которых уравнение выполняется, мы ищем нули функции.
Кроме того, нули функции играют важную роль в определении характеристик функции. Например, они позволяют нам определить параболу, гиперболу или эллипс. Зная нули функции, мы можем оценить, как поведет себя функция в разных частях области определения.
Нули функции используются не только в математике, но и в физике. Они позволяют нам решать задачи, связанные с движением тела, определение равновесия или поиск точек перегиба.
| Применение нулей функции | Пример |
| Нахождение корней уравнений | Нули функции f(x) = x^2 - 4x + 3 = 0 определют его решения |
| Определение типа функции | Нули функции f(x) = x^2 - 1 определют, что это парабола |
| Анализ движения тела | Нули функции f(t) = 0.5gt^2 + vt + h определют моменты времени, в которые тело находится в положении покоя |
Таким образом, нули функции являются важными элементами в математике и физике, они помогают решать уравнения, определять характеристики функций и решать различные физические задачи.
Способы поиска нулей функции
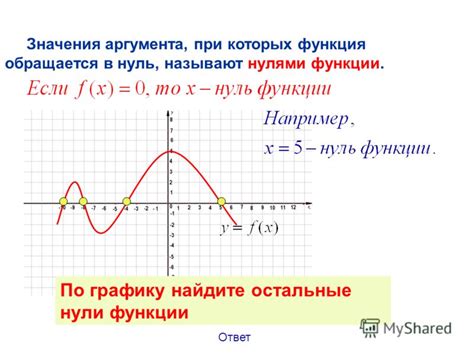
Существует несколько способов для определения нулей функции:
| Способ | Описание |
|---|---|
| Метод подстановки | Заключается в подстановке различных значений аргумента функции и нахождении соответствующих значений функции. Если полученное значение функции равно нулю, то это будет нулевая точка функции. |
| Графический метод | Построение графика функции и определение точек пересечения графика с осью абсцисс. Это будут нулевые точки функции. |
| Метод деления отрезка пополам (бисекции) | Этот метод основывается на свойстве непрерывности функции. Задается начальный отрезок, на котором функция меняет знак, и затем отрезок последовательно делится пополам до достижения необходимой точности. Нулевая точка функции находится в пределах конечного отрезка. |
| Метод Ньютона (касательных) | Данный метод основывается на использовании производной функции и последовательном приближении к нулевой точке с помощью касательных. |
Выбор способа поиска нулей функции зависит от конкретной задачи, доступных данных и требуемой точности определения нулевых точек функции.
Метод графика
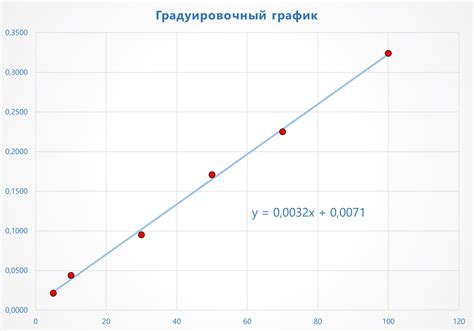
Для построения графика функции необходимо задать значения аргумента и соответствующие им значения функции и отобразить их на координатной плоскости. После этого следует проанализировать график и найти точки пересечения с осью абсцисс, которые и являются искомыми нулями функции.
Основная идея этого метода заключается в том, что при переходе от одного значения аргумента к другому, значение функции также изменяется. Если при изменении аргумента функция меняет свой знак, то точка пересечения графика с осью абсцисс будет являться нулем функции.
Однако следует помнить, что метод графика может быть эффективен только в случае, когда функция имеет простой и наглядный график. В противном случае может потребоваться использование других методов поиска нулей функции.
Для использования метода графика необходимы навыки работы с геометрическим построением и умение анализировать графики функций. Кроме того, этот метод требует наличия координатной плоскости и инструментов для ее построения, например, бумаги и линейки, или программного обеспечения для графического моделирования функций.
Метод подстановки

Для применения метода подстановки необходимо знать область определения функции и ее аналитическое выражение. Затем выбираются различные значения аргумента, которые подставляются в выражение функции. Результат подстановки сравнивается с нулем.
Если результат подстановки равен нулю, то это значение аргумента является нулем функции. Если результат не равен нулю, то выбирается другое значение аргумента и процедура повторяется.
Преимуществами метода подстановки являются его простота и доступность. Однако он может быть неэффективным при сложных функциях или большом количестве возможных значений аргумента.
В некоторых случаях метод подстановки может быть использован в сочетании с другими методами поиска нулей функции для уточнения результатов.
Метод итераций

Алгоритм работы метода итераций выглядит следующим образом:
- Выбирается некоторое начальное приближение для корня функции.
- Вычисляется значение функции в выбранной точке.
- На основе полученного значения функции строится новое приближение для корня функции.
- Шаги 2 и 3 повторяются до достижения требуемой точности результата.
Основным преимуществом метода итераций является его простота и универсальность - он может применяться для любых функций, как линейных, так и нелинейных.
В то же время, метод итераций требует определенного уровня начального приближения, чтобы процесс приближения не расходился. Также он может иметь сравнительно низкую скорость сходимости по сравнению с другими методами, такими как метод половинного деления или метод Ньютона.
Тем не менее, метод итераций все еще является одним из самых популярных и широко используемых численных методов для поиска нулей функции. Он находит применение в различных областях, включая математику, физику, инженерию и экономику.
Метод дихотомии
Применение метода дихотомии состоит из следующих шагов:
- Выбор начального отрезка, включающего искомый корень.
- Вычисление значения функции в середине отрезка и определение, в какой половине отрезка находится корень.
- Сужение отрезка до нужной половины на основе полученной информации.
- Повторение шагов 2 и 3 до достижения требуемой точности.
- Возврат найденного значения корня.
Преимущества метода дихотомии заключаются в его простоте, надежности и гарантированной сходимости к решению. Кроме того, он может быть использован для функций любой формы, если они удовлетворяют условию непрерывности.
Однако метод дихотомии может быть медленным, особенно для функций, которые имеют быстро меняющуюся производную или множественные корни. Также он требует начального приближения отрезка, содержащего корень, что может потребовать дополнительных вычислений.
В целом, метод дихотомии является одной из базовых техник численного решения уравнений и может быть использован в сочетании с другими методами для повышения эффективности и точности поиска нулей функции.
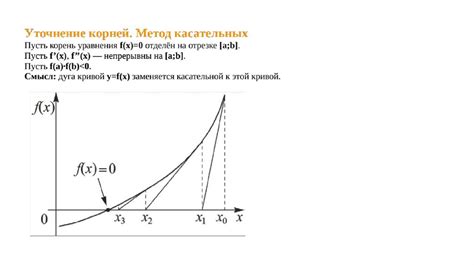
Метод Ньютона

Для применения метода Ньютона необходимо задать начальное приближение решения и провести итерационный процесс до достижения заданной точности. Каждая итерация метода включает вычисление значения функции и ее производной в текущей точке, а затем определение следующего приближения решения.
Преимущество метода Ньютона заключается в его высокой скорости сходимости. Он позволяет быстро находить корни функций, особенно в случае, когда начальное приближение достаточно близко к решению.
Один из недостатков метода Ньютона - его чувствительность к начальному приближению. Неправильный выбор начального значения может привести к расхождению метода или нахождению локальных минимумов и максимумов функции, вместо корней.
Таблица 1. Алгоритм метода Ньютона
| Шаг | Описание |
|---|---|
| 1 | Задать начальное приближение $x_0$ и точность $\epsilon$ |
| 2 | Вычислить значение функции $f(x_0)$ и ее производной $f'(x_0)$ |
| 3 | Вычислить приближение следующего значения $x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}$ |
| 4 | Проверить условие окончания итераций: $|x_1 - x_0| |
| 5 | Если условие выполнено, то решение найдено: $x_1$ является приближенным значением корня функции |
| 6 | Иначе присвоить $x_0$ значение $x_1$ и перейти к шагу 2 |
Метод Ньютона широко используется для решения уравнений и поиска корней функций, а также в задачах оптимизации и анализе данных. Однако его применение требует осторожности и проверки полученных результатов на адекватность.