Принадлежность прямой к плоскости – это важное понятие, которое часто используется в геометрии и аналитической геометрии. Как доказать, что прямая лежит в плоскости? Существует несколько методов, которые помогут ответить на этот вопрос.
Один из самых простых методов – это использование уравнения плоскости и параметрического уравнения прямой. Если подставить координаты точки прямой в уравнение плоскости и получим верное равенство, то прямая принадлежит плоскости. Этот метод является надежным и часто применяется при решении задач геометрии.
Рассмотрим пример: дана плоскость со следующим уравнением: 2x - 3y + 5z - 7 = 0, и прямая с параметрическим уравнением: x = 1 + t, y = 2 - 2t, z = 3t. Чтобы доказать принадлежность прямой к плоскости, заменяем x, y и z в уравнение плоскости на значения из уравнения прямой:
2(1 + t) - 3(2 - 2t) + 5(3t) - 7 = 0
Упрощаем уравнение и получаем:
2 + 2t - 6 + 6t + 15t - 7 = 0
23t - 11 = 0
Решаем полученное уравнение и находим значение t:
t = 11/23
Подставляем найденное значение t в параметрическое уравнение прямой и получаем координаты точки, принадлежащей и прямой, и плоскости:
x = 1 + 11/23, y = 2 - 2(11/23), z = 3(11/23)
Таким образом, мы нашли точку, которая принадлежит как прямой, так и плоскости. Это означает, что прямая принадлежит плоскости.
Как доказать принадлежность прямой к плоскости

- Метод координат. В этом методе используются координаты точек, принадлежащих прямой и плоскости. Если для всех точек прямой и плоскости выполнено уравнение плоскости, то прямая принадлежит данной плоскости.
- Метод перпендикулярности. Если прямая перпендикулярна всем прямым, лежащим в данной плоскости, то она принадлежит этой плоскости. Для проверки перпендикулярности прямой к плоскости можно использовать скалярное произведение векторов.
- Метод выпуклости. Если прямая лежит внутри выпуклой оболочки точек плоскости, то она принадлежит этой плоскости. Для проверки выпуклости можно использовать алгоритм Грэхема для поиска выпуклой оболочки.
Приведем пример доказательства принадлежности прямой к плоскости с использованием метода координат:
Пусть даны точки A(1, 2, 3), B(2, 4, 5) и C(3, 6, 7), принадлежащие прямой, а также уравнение плоскости 2x + 3y - z = 4. Для каждой точки прямой подставим ее координаты в уравнение плоскости:
- Точка A: 2*1 + 3*2 - 3 = 4 - 3 = 1
- Точка B: 2*2 + 3*4 - 5 = 4 + 12 - 5 = 11
- Точка C: 2*3 + 3*6 - 7 = 6 + 18 - 7 = 17
Если для всех точек прямой выполнено уравнение плоскости, то прямая принадлежит данной плоскости. В этом примере уравнение плоскости выполняется для всех точек (A, B, C), следовательно, прямая принадлежит данной плоскости.
Методы доказательства

Существует несколько методов, которые позволяют доказать принадлежность прямой к плоскости:
1. Аналитический метод. Для доказательства принадлежности прямой к плоскости можно воспользоваться аналитическим методом. Для этого необходимо представить уравнение плоскости в координатной форме и затем подставить координаты точек прямой в это уравнение. Если после подстановки выполняется тождество, то прямая принадлежит плоскости.
2. Геометрический метод. Другой способ доказательства заключается в использовании геометрического метода. Для этого можно построить плоскость и прямую на геометрической плоскости и затем проверить, лежит ли прямая на данной плоскости. Если прямая находится внутри плоскости или совпадает с ней, то они принадлежат друг другу.
3. Векторный метод. Векторный метод основан на анализе векторов, которые определяют прямую и плоскость. Для доказательства принадлежности прямой к плоскости можно рассмотреть векторы, задающие прямую, и векторы, задающие плоскость. Если векторы принадлежат одной плоскости или параллельны ей, то прямая принадлежит плоскости.
Выбор метода доказательства зависит от конкретной задачи и доступных данных. Каждый из методов имеет свои преимущества и может быть использован в различных случаях.
Метод планировки
Процесс планировки начинается с выбора плоских фигур, которые можно построить на плоскости и имеют общие элементы с прямой и плоскостью. Затем эти фигуры изображаются на плоскости и проводится анализ их взаимного расположения. Если среди выбранных фигур содержатся и прямая, и плоскость, их взаимное расположение дает основание предполагать, что прямая принадлежит плоскости.
Метод планировки может быть использован, например, для доказательства принадлежности прямой к плоскости задачами, где требуется проверить, пересекается ли плоскость с данной прямой или проходит через нее. В таких случаях планировка может помочь увидеть взаимное расположение прямой и плоскости и убедиться в их пересечении или совпадении.
Метод планировки является эффективным инструментом для доказательства принадлежности прямой к плоскости, так как он сочетает в себе логический анализ и наглядную иллюстрацию. При использовании этого метода важно выбирать правильные плоские геометрические фигуры и проводить аккуратные и точные построения во избежание ошибок.
Метод наклонения
Чтобы применить метод наклонения, необходимо знать угловой коэффициент прямой и угол наклона плоскости. Угловой коэффициент прямой можно найти по формуле k = tg α, где α – угол наклона прямой.
Если же угловой коэффициент прямой не равен тангенсу угла наклона плоскости, то прямая не принадлежит плоскости. Такая прямая называется "скользящей" по плоскости.
Применение метода наклонения позволяет эффективно доказывать принадлежность прямой к плоскости, используя геометрические особенности данных объектов. Этот метод находит широкое применение в геометрии и строительстве, а также при решении различных задач по аналитической геометрии.
Метод сечения
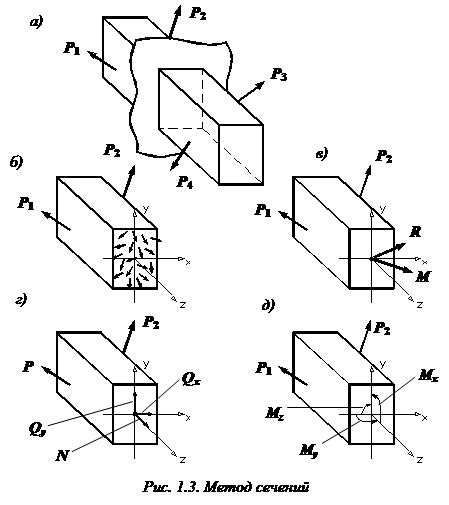
Примеры доказательства
Пример 1:
Пусть дана плоскость P: 2x + 3y - z = 5 и прямая l, заданная системой уравнений: x = 1 + 2t, y = 3 + 4t, z = -2 + t.
Чтобы доказать, что прямая l принадлежит плоскости P, нужно подставить параметрические уравнения прямой l в уравнение плоскости P и проверить, выполняется ли равенство.
Подставим значения x, y и z в уравнение плоскости:
2(1 + 2t) + 3(3 + 4t) - (-2 + t) = 5
Упростим это уравнение:
2 + 4t + 9 + 12t + 2 - t = 5
15t + 13 = 5
15t = -8
t = -8/15
Таким образом, найдено значение параметра t, при котором прямая l принадлежит плоскости P.
Пример 2:
Пусть дана плоскость P: x - y + 2z = 0 и прямая l, заданная системой уравнений: x = -3 + t, y = 1 - t, z = 2t.
Чтобы доказать, что прямая l принадлежит плоскости P, можно воспользоваться свойством ортогональности нормали плоскости к прямой. Запишем вектор нормали плоскости как (1, -1, 2), а направляющий вектор прямой как (1, -1, 2).
Проверим ортогональность векторов:
(1, -1, 2) * (1, -1, 2) = 1 * 1 + (-1) * (-1) + 2 * 2 = 1 + 1 + 4 = 6
Так как произведение скалярное равно 6, векторы не ортогональны, и прямая l не принадлежит плоскости P.
Пример 3:
Пусть дана плоскость P: 2x + y - z = 4 и прямая l, заданная системой уравнений: x = 1 + t, y = 2 + 2t, z = -1 - t.
Для доказательства принадлежности прямой l к плоскости P нужно найти такое значение параметра t, при котором выполняется уравнение плоскости. Подставим значения x, y и z в уравнение плоскости:
2(1 + t) + (2 + 2t) - (-1 - t) = 4
Упростим это уравнение:
2 + 2t + 2 + 4t + 1 + t = 4
7t + 5 = 4
7t = -1
t = -1/7
Таким образом, найдено значение параметра t, при котором прямая l принадлежит плоскости P.
Пример 1: Доказательство методом планировки
Пусть дана прямая AB и плоскость Г, и необходимо доказать, что прямая AB принадлежит плоскости Г.
1. Возьмем произвольную точку C на прямой AB и проведем через нее плоскость, перпендикулярную плоскости Г.
2. Пусть эта плоскость обозначается как П.
3. Так как прямая AB лежит в плоскости П, то она пересекает плоскость Г в точке D.
4. Следовательно, прямая AB принадлежит плоскости Г.
Таким образом, мы доказали, что прямая AB принадлежит плоскости Г с использованием метода планировки.
Пример 2: Доказательство методом наклонения
Для доказательства принадлежности прямой к плоскости существует метод наклонения. Этот метод основан на том, что прямая принадлежит плоскости, если все прямые, параллельные данной прямой и проходящие через точки на данной прямой, лежат в этой плоскости.
Рассмотрим пример. Дана плоскость Π и прямая l. Наша задача - доказать принадлежность прямой l к плоскости Π.
Для этого выберем множество точек на прямой l, например, точки A, B и C.
Теперь проведем прямые, параллельные прямой l и проходящие через эти точки. Пусть прямые m и n проходят через точку A, прямые p и q проходят через точку B, а прямые s и t проходят через точку C.
Таким образом, используя метод наклонения, мы можем доказать принадлежность прямой к плоскости.
Пример 3: Доказательство методом сечения
Рассмотрим пример. Даны прямая АВ и плоскость МНК. Необходимо доказать, что прямая АВ принадлежит плоскости МНК.
Шаг 1: Построим плоскость, проходящую через прямую АВ и перпендикулярную плоскости МНК. Для этого возьмем произвольную точку С на прямой АВ. Проведем через эту точку прямую, перпендикулярную к плоскости МНК, и найдем пересечение этой прямой с плоскостью МНК. Обозначим полученную точку пересечения как D.
Шаг 2: Докажем, что прямая АВ пересекает полученную плоскость МНК в точке D. Для этого достаточно доказать, что точка D лежит как на плоскости МНК, так и на прямой АВ. Точка D уже определена как точка пересечения прямой, перпендикулярной плоскости МНК, с самой плоскостью МНК. А точка С лежит на прямой АВ, поскольку она выбрана на этой прямой. Таким образом, точка D принадлежит и плоскости МНК, и прямой АВ.
Таким образом, мы доказали, что прямая АВ принадлежит плоскости МНК методом сечения. Этот метод может быть использован для доказательства принадлежности прямой к плоскости в различных геометрических задачах.